Thiết lập phương trình Euler tĩnh

Trong bài này mình sẽ giấy thiệu về cách xây dựng phương trình vi phân cân bằng của chất lỏng tĩnh, hay còn gọi là phương trình Euler tĩnh. Sau đó từ phương trình vi phân thu được, chúng ta tìm nghiệm của phương trình này bằng phương pháp tích phân trong một số trường hợp đơn giản.

Chúng ta đã biết là trong môi trường chất lỏng tĩnh ( không có sự chuyển động tương đối giữa các lớp chất lỏng). Tác dụng lên chất lỏng chỉ có thành phần lực khối.

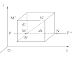
Để xây dựng phương trình Euler tĩnh, chúng ta chọn hệ trục tọa độ gắn chặt với bình bể chất lỏng. Trong môi trường chất lỏng tĩnh lấy một điểm M bất kỳ có tọa độ x, y ,z và có áp suất p (Hình 1).

Hình 1

Tách ra một khối chất lỏng có dạng hình hộp chứ nhật, có các cạnh song song với các trục tọa độ, có độ dài tương ứng là dx, dy, dz. Điểm M là một đỉnh của hình hộp chữ nhật. Xét điều kiện cân bằng của khối chất lỏng được tách ra. Giả sử khối chất lỏng chịu sự tác động lực khối tổng hợp từ 3 thành phần theo phương các trục Ox, Oy, Oz. Lực khối đơn vị theo các trục tương ứng là X, Y, Z. Khi đó lực khối thành phần theo từng phương trục tọa độ bằng tích khối lượng của khối chất lỏng nhân với lực khối đơn vị tương ứng.

Áp suất trong lòng khối chất lỏng là một hàm không gian, tức là p=p(x,y,z). Theo tính chất của áp suất thủy tĩnh tại điểm M giá trị áp suất bằng nhau theo mọi phương, giả sử tại M có áp suất là p_M. Khi di chuyển điểm M tới điểm N. Theo phương Ox tọa độ điểm M thay đổi một lượng dx. Kéo theo đó hàm p(x,y,z) biến thiên một lượng bằng vi phần từng phần (∂p/∂x)dx, vì vậy áp suất tại điểm N là p_M+(∂p/∂x)dx.

Ở đó (∂p/∂x) – được gọi là gradient áp suất điểm M theo phương Ox.

Xét các cặp điểm tương ứng trên 2 mặt giới hạn vuông góc với Ox của khối chất lỏng, ví dụ M’ và N’, ta đều thấy rằng giữa các cặp điểm này khác nhau một lượng áp suất.

$p - \left( {p + \frac{{\partial p}}{{\partial x}}dx} \right) = - \frac{{\partial p}}{{\partial x}}dx$

Vậy chênh lệch áp lực giữa 2 mặt giới hạn vuông góc với Ox của khối chất lỏng là tích của lượng chênh áp nhân với diện tích của 1 mặt.

${F_{ca}} = - \frac{{\partial p}}{{\partial x}}dxdydz$

Tác dụng lên khối chất lỏng theo phương Ox có 2 thành phần lực: lực khối và lực chênh áp giữa 2 mặt giới hạn của khối hình hộp.

Lực khối theo phương Ox là:

F_kx=Xρdxdydz

Xét cân bằng của khối chất lỏng theo phương Ox:

$\begin{array}{l} {F_{kx}} + {F_{ca}} = 0\\ X\rho dxdydz - \frac{{\partial p}}{{\partial x}}dxdydz = 0 \end{array}$

Tương tự trên các phương Oy, và Oz ta có:

$Y\rho dxdydz - \frac{{\partial p}}{{\partial y}}dxdydz = 0$

$Z\rho dxdydz - \frac{{\partial p}}{{\partial z}}dxdydz = 0$

Tương đương với:

$X - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} = 0$

$Y - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} = 0$ (1.1)

$Z - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} = 0$

Hệ 3 phương trình (1.1) là phương trình Euler tĩnh ở dạng vi phần từng phần.

Cộng theo vế 3 phương trình trên ta được:

$Xdx + Ydy + Zdz - \frac{1}{\rho }\left( {\frac{{\partial p}}{{\partial x}}dx + \frac{{\partial p}}{{\partial y}}dy + \frac{{\partial p}}{{\partial z}}dz} \right) = 0$

Ta thấy tích phân toàn phần áp suất:

$dp = \left( {\frac{{\partial p}}{{\partial x}}dx + \frac{{\partial p}}{{\partial y}}dy + \frac{{\partial p}}{{\partial z}}dz} \right)$

Suy ra ta có:

dp=ρ(Xdx+Ydy+Zdz) (1.2)

Phương trình (1.2) là phương trình Euler tĩnh ở dạng toàn phần.

Xét một số trường hợp đơn giản.

Trường hợp 1 :

Môi trường chất lỏng đứng yên chỉ chịu tác dụng của trọng lực.

Khi đó lực khối đơn vị Z= –g ; Y=X=0.

Ta có phương trình vi phân cân bằng :

dp= –ρgdz

Lấy tích phân ta có

p= –ρgz+C

C – hằng số tích phân

Suy ra : z+p/(ρg)=const
Đây chính là phương tình cơ bản thủy tĩnh học. Mời các bạn đọc thêm bài: Phương trình thủy tĩnh học cơ bản

Trường hợp 2:

Chuyển động quay tròn đều quanh trục đứng của bình chứa chất lỏng.

Bình chứa chất lỏng mở quay đều với vận tốc góc ω quanh trục đứng của bình. Quan sát hiện tượng thấy chất lỏng cũng quay theo bình với cùng vận tốc ω; mặt thoáng của chất lỏng trong bình ở trung tâm hạ thấp xuống và ở mép thì nâng cao lên. Mặt thoáng của chất lỏng trong bình trở thành mặt dạng tròn xoay. Tác dụng lên khối chất lỏng trong trường hợp này có hai lực khối – trọng lực và lực ly tâm, tương ứng với 2 lực khối đơn vị là g và ω²r.

Áp dụng phương trình (1.2) để xác định qui luật thay đổi áp suất trong trường hợp này. Ta có:

Z= –g; X= ω²rcos(r,x) = ω²x; Y= ω²rcos(r,y)=ω²y; với x²+y²=r²

Thế vào phương trình (1.2) ta có :

dp=ρ(ω²xdx+ ω²ydy – gdz)

Lấy tích phân 2 vế thu được :

p= ρ ω²(x²+y²)/2 – ρgz +C

p= ρ ω²r²/2– ρgz +C

C – hằng số tích phân

Khi r=0, z=h, p=p_at ta có : p_at= – ρgh+C

Suy ra C=p_at+ ρgh

Vậy p= ρ ω²r²/2– ρgz+ p_at+ ρgh

p= p_at+ ρ ω²r²/2+ ρg(h – z)

Để xác định phương trình mặt thoảng của chất lỏng trong bình ta có

p= p_at

Suy ra : z=h+ ω²r²/(2g)

Hình 2

Như vậy đường cong AOB có dạng parabol. Mặt thoáng của chất lỏng có dạng parabol tròn xoay. Sử dụng phương trình trên có thể xác định được vị trí mặt thoáng của chất lỏng trong bình, và xác định được chiều cao h của vị trí đỉnh parabol nếu biết vận tốc góc ω. Để làm được điều đó phải sử dụng phương trình bảo toàn thể tích: thể tích khối chất lỏng khi đứng yên bằng thể tích khối chất lỏng khi xoay.
Bài viết hôm nay của mình tạm dừng tại đây.
Chúc cả nhà vui vẻ cuối tuần!

Điểm 4.6/5 dựa vào 87 đánh giá

SmartPay : Mở ví điện tử đơn giản tiện lợi Click xem
Pierre Cardin : Sale off cuối năm 50% Click xem
MB Android : Miễn phí chuyển khoản tới tất cả các ngân hàng Click xem