Áp lực chất lỏng lên thành phẳng

Trong xây dựng thủy lợi, xây dựng đê đập kênh mương, hoặc khi xây dựng các bể chứa luôn cần tính toán áp lực tác dụng của chất lỏng lên thành chứa. Trong bài này mình sẽ trình bày và phân tích cách xây dựng công thức tính toán áp lực lên thành phẳng trong Thủy tĩnh học.Đây cũng chính là cơ sở để giải các bài tập thủy tĩnh học cơ bản.

Trong bài này có sử dụng kiến thức về mômen tĩnh và mômen quán tính của tiết diện ngang. Bạn nào cần tìm hiểu có thể tải file này về tìm hiểu: 

• Đặc trưng hình học(RAR) 
• Download Bài viết (PDF)

Bây giờ chúng ta đi nghiên cứu bài toàn này.

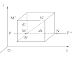
I. Bài toán

Sử dụng phương trình cơ bản thủy tĩnh học để xác định áp lực tổng hợp của chất lỏng lên thành phẳng, nằm nghiêng với phương ngang 1 góc α (hình vẽ). Chúng ta cần tính áp lực F tác dụng từ hướng chất lỏng lên 1 phần của thành phẳng, được giởi hạn bởi chu tuyến (đường cong kín) có diện tích bằng S.

 

Hinh 1. Sơ đồ tính áp lực lên thành phẳng

Trục Ox hướng theo đường giao tuyến giữa thành phẳng với mặt thoáng của chất lỏng, trục Oy vuông góc với trục Ox và nằm trong mặt phẳng của thành phẳng.

Trước hết cần xác định thành phần áp lực tác dụng lên phần diện tích vô cùng nhỏ dS:

dF=pdS=(p_o+ρgh)dS= p_odS+ρghdS ;

Ở đó: p_o – áp suất tại mặt thoáng chấ lỏng; h – độ sâu từ mặt thoáng tới phần diện tích dS.

Để xác định áp lực toàn phần ta cần lấy tích phân dF theo toàn bộ diện tích S.

Ta có:

Ở đó y – tọa độ diện tích dS.

Tích phân cuối là momen tĩnh của diện tích S đối với trục Ox và bằng diện tích của nó nhân với tọa độ tâm khối.

Suy ra ta có:

F = p_oS + ρgh_CS ; (1.1)

Với công thức (1.1) này ta có thể nghiệm chứng lại định luật Pascal « Chất lỏng truyền áp suất nguyên vẹn theo mọi hướng » . Ở đây ta thấy môi trường chất lỏng đã truyền áp suất p₀ trên bề mặt thoáng chất lỏng nguyên vẹn tới mọi điểm trên mặt phẳng S. Nếu p₀ thay đổi 1 lượng ∆p thì tương ứng tại mỗi điểm trên mặt S áp suất cũng thay đổi một lượng ∆p. ( Đây chính là ý nghĩa của định luật Pascal)

Ở đó h_C – độ sâu của tâm khối của diện tích S, h_C = y_C∙sinα;

Hay F=(p_o + ρgh_C)S=p_CS   (1.2)

Phát biểu cho công thức (1.2): Áp lực toàn phần của chất lỏng lên thành phẳng bằng tích diện tích thành phẳng nhân với áp suất thủy tĩnh tại tâm khối của thành phẳng đó.

Nhận xét

1. Theo công thức (1.1) ta có thể coi thành phần ρgh_CS là áp lực sinh ra bởi chính chất lỏng, còn thành phần p_oS là áp lực sinh không phải bởi chất lỏng. Trong trường hợp tổng quát áp lực tổng hợp thành phẳng phải chịu chính là tổng hợp 2 thành phần lực: thành phần lực sinh ra bởi chất lỏng F_cl và thành phần lực sinh ra không phải do chất lỏng F_n. Với F_n ta hiểu nó không phải sinh ra do mỗi áp suất p₀ như trường hợp trên, mà còn phải kể tới do các ngoại lực khác, từ các hướng khác nhau nữa. Riêng thành phần F_cl = ρgh_C về mặt độ lớn F_cl tương đương với trọng lượng P_cl của khối chất lỏng giới hạn bởi một trụ đứng chiều cao h_C, diện tích 2 mặt đáy là S. ( Lưu ý: nói trụ đứng ở đây cần hiểu không nhất thiết phải là trụ tròn, vì  S có thể có hình dạng bất kỳ – miễn là bao trong 1 chu tuyến kín)

2.Theo công thức (1.2) ta đưa ra khái niệm áp lực dư F_dư = p_C.dưS.
Trong các trường hợp khi áp suất p_o=p_atm , và cũng tác động lên mặt ngoài của thành phẳng. Lúc này thành phần lực sinh ra do áp suất khi quyển ở 2 mặt trước và sau thành cân bằng, nên có độ lớn bằng 0.

Khi đó áp suất dư tại tâm khối p_C.dư = p_C – p_atm = ρgh_C . Thành phẳng phải chịu tác động áp lực toàn phần tác động lên thành phẳng bằng trọng lượng của khối chất lỏng.

Theo biểu thức p_C.dưS = ρgh_CS hay F_dư = P_cl .

II. Xác định điểm đặt của áp lực toàn phần.

Như vậy ngoại áp lực sinh ra bởi p₀ tại tất cả cả điểm diện tích S là như nhau, do đó lực tổng hợp sinh ra F₀ – sẽ đặt vào trọng tâm của diện tích S. Để xác định điểm đặt sinh ra bởi áp lực F_cl – sinh ra do khối lượng chất lỏng, chúng ta sử dụng lý thuyết cơ học (Cơ lý thuyết). Khi đó mômen tổng hợp lực đối với trục Ox bằng tổng mômen các thành phần lực.

y_D – tọa độ điểm đặt trọng lực khối chất lỏng.

 

Với  

Suy ra  

J_x = J_x0 + y­²_CS;

 J_x0 – momen quán tính của diện tích S so với trục đi qua trọng tâm C song song với Ox.

y_D = y_C + J_x0/ (y_CS)   (1.3)

Như vậy điểm đặt của lực F_cl – ở thấp hơn tâm khối của diện tích thành phẳng và cách 1 khoảng là

∆y=J_x0/(y_CS)

Khi áp suất p₀ = p_atm, và thành ngoài cũng chịu tác động của p_atm , thì điểm D sẽ là điểm đặt tổng hợp lực lên thành (do áp lực sinh ra 2 phía thành khử nhau). Khi p_o ≠ p_atm , điểm đặt của tổng hợp lực: F₀  và F_cl  xác định theo qui luật cơ học – cân bằng mômen; Khi đó F₀ càng lớn, điểm đặt của tổng hợp lực càng gần trọng tâm C.

Điểm 4.6/5 dựa vào 42 đánh giá

• SmartPay : Mở ví điện tử đơn giản tiện lợi Click xem
• Pierre Cardin : Sale off cuối năm 50% Click xem
• MB Android : Miễn phí chuyển khoản tới tất cả các ngân hàng Click xem